Wat is 2048?
Het spel 2048 is een schuifpuzzel op een raster van 4×4 dat begint met twee tegels op het speelveld. Deze twee tegels bevatten een score van 2 (met 90% kans) of een score van 4 (met 10% kans) en kunnen op elk willekeurige plek van het raster belanden. Na deze initialisatie kan het spel beginnen. Elke zet heeft de speler vier keuze opties om te doen: omhoog, omlaag, links en rechts. Na elke zet komt er een nieuwe tegel (waarde 2 of 4, met 90/10 kansverdeling) op een willekeurige beschikbare plek op het raster. Het doel van het spel is om een tegel met de waarde 2048 te krijgen. Het verkrijgen van hogere waardes gebeurt door het combineren van tegels met dezelfde waardes. Het voorbeeld hieronder geeft dit grafisch weer.
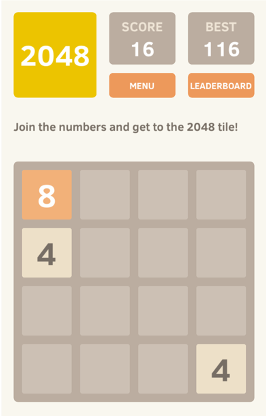
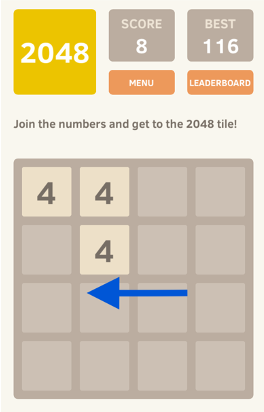
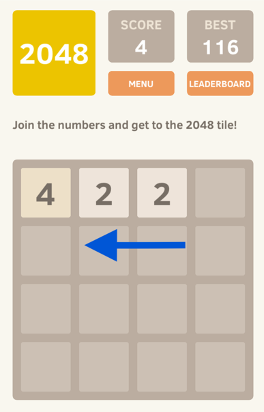
Het spel is voorbij wanneer het raster vol is en er geen zetten meer mogelijk zijn (omhoog, omlaag, links of rechts).
Genetische algoritmen
Genetische algoritmen zijn gebaseerd op de evolutietheorie van Darwin, waarin natuurlijke selectie plaatsvindt gebaseerd op de fitness van een individu (Survival of the fittest). Het doel van deze algoritmen is het optimaliseren van wiskundige functies. Een typisch genetisch algoritme bestaat uit verschillende onderdelen:
- Populatie bestaande uit N individuen
- Fitness functie manier van evalueren van het individu
- Crossover manier van individuen combineren
- Mutatie manier van muteren van een individu
Deze vier aspecten werken als volgt samen. Initialiseer de start populatie (vaak willekeurig gegenereerd) en definieer de fitness functie. Vervolgens wordt elk individu in de populatie door middel van de fitness functie geëvalueerd. De individuen met de beste fitness worden vervolgens gekozen om zich voort te planten en de overige individuen verlaten de populatie. Het voortplanten van de gekozen beste individuen wordt gedaan door middel van crossover. De ‘kindjes’ die hieruit ontstaan kunnen vervolgens gemuteerd worden om diversiteit in de populatie te behouden. Op dit moment in het proces beschikken we opnieuw over een volledige, deels vernieuwde, populatie en belanden we in een nieuwe generatie. Voor elke nieuwe generatie wordt het proces van fitness evaluatie, ouder selectie, crossover en mutatie herhaald totdat de gewenste fitness of het maximum aantal generaties behaald is.
Eén van de voordelen van het gebruik van een genetisch algoritme is dat het snel een goede oplossing kan vinden, maar een nadeel is dat dit niet gegarandeerd de optimale oplossing is.
Genetische algoritmen + neurale netwerken
Maar hoe train je neurale netwerken met een genetisch algoritme? Een neuraal netwerk is in feite een wiskundige formule die, afhankelijk van de netwerkstructuur, enorm groot en complex kan zijn. Deze formule is vervolgens opgebouwd uit de gewichten van het netwerk, de biases van de neuronen en de gebruikte activatie functies. Onderstaand figuur geeft dit grafisch weer.
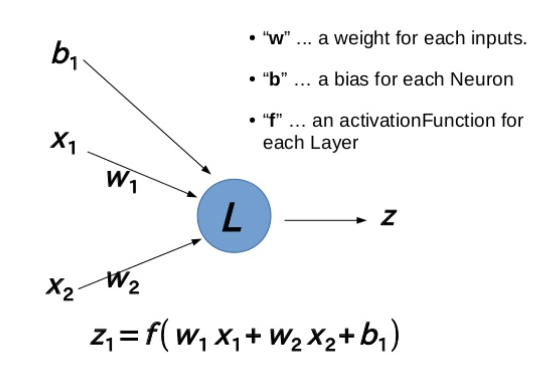
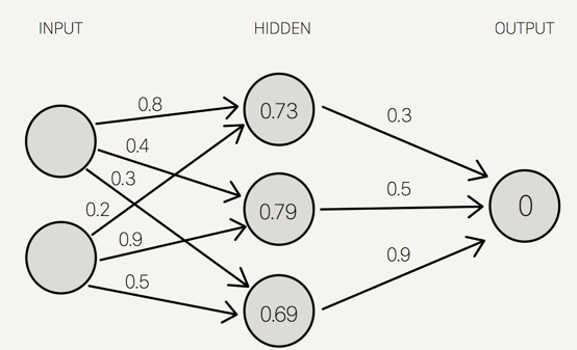
De resulterende functie kan vervolgens geoptimaliseerd worden door middel van het optimaliseren van de gewichten en de biases. Ook is het mogelijk om tegelijkertijd de netwerkstructuur te optimaliseren met behulp van bijvoorbeeld NeuroEvolution of Augmenting Topologies (NEAT). Om vervolgens gebruik te maken van het genetische algoritme is het belangrijk om het netwerk op een handige manier weer te geven. Hieronder is een voorbeeld gegeven van een mogelijke weergave, waarbij de blauwe getallen de gewichten zijn en de oranje de biases.

Over op de praktijk
Hoe gaan we de opgedane kennis toepassen om een bot te creëren die zelfstandig, en zo goed mogelijk, het spel 2048 kan spelen. Voor het initialiseren van de netwerken is het van belang om te weten wat we gaan gebruiken als input en wat we als output verwachten. Voor het bepalen van de fitness functie is het belangrijk om te achterhalen wat het beste bij dit probleem past. Voor crossover is het belangrijk om te weten wat voor een probleem we hebben. Bestaat dit uit categorische (binair of niet binair) of continue waardes. Mutatie is belangrijk voor het bepalen van hoeveel toeval in de populatie gewenst is. Bij het bepalen van deze criteria helpt het om goed van tevoren na te denken, maar trial en error blijft in veel gevallen nodig.
De gebruikte waardes en methoden voor het maken van de 2048 bot zijn als volgt:
- Populatie: 200 netwerken, waarbij:
- Netwerk input: State van het speelveld (4×4 = 16 input nodes) + een teller die de vastzit hoeveelheid aangeeft (1 input node) + de mogelijke zetten (4 input nodes)
- Netwerk output: 4 keuze opties elke beurt 4 output nodes
- Hidden layer: 1 hidden layer van 10 nodes (experimenteel bepaald)
- Fitness functie Som van de 2 maximale waardes in het veld – een vastzit straf
- Crossover combinatie van n-point crossover + arithmetic function
- Mutatie 20% kans op mutatie
Resultaten
In dit filmpje is te zien dat de bot overduidelijk een strategie heeft aangeleerd, maar dat de bot niet altijd even verstandige keuzes maakt. Zo kan hij bepaalde, hoog scorende, zetten eerder in het proces doen om zo het spel sneller en efficiënter naar een hoge tegel te leiden. Daarnaast is de gehele tijd het veld vrij vol met tegels. Dit komt gevaarlijk over, maar dit kan ook een manier van de bot zijn om de willekeurigheid van elke nieuwe tegel te verkleinen. Wanneer we de bot 1000 verschillende spellen laten spelen komen we uit op de volgende resultaten tabel.
| Max tegel | 32 | 64 | 128 | 256 | 512 | 1024 |
| Aantal keer behaald | 1 | 13 | 112 | 441 | 392 | 41 |
De gemiddelde score was: 5000,552
Het gemiddelde aantal zetten was: 393,786
Jammer genoeg heeft de bot geen één keer de targetscore van 2048 gehaald. Het behalen van 2048 is wel een aantal keer gelukt gedurende het trainingsproces, maar dit lijkt meer op toeval te berusten dan op het leren van een strategie die goed genoeg is om regelmatig het spel uit te spelen. De bot weet wel gemiddeld gezien bijna 400 zetten te overleven en haalt een gemiddelde score van ongeveer 5000 punten. In mijn optiek is de performance nog niet geweldig, maar dat was ook niet het hoofddoel van dit project. Het is duidelijk te zien dat de bot een tactiek leert en zich redelijk staande kan houden.
Problemen/Learnings
Het eerste probleem dat zich voordeed was wanneer een zet voorspeld werd die niet mogelijk was. Omdat er niks in het veld verandert zal het netwerk altijd dezelfde output geven en dus eigenlijk vastlopen. Om dit op te lossen is in de fitness functie een grote straf gezet op het vastlopen. Dit verplicht het model om de strategie aan te passen en altijd een valide output te geven.
Daarnaast was de train tijd in het begin erg lang. Dit is een probleem dat wel vaker terugkomt bij het gebruik van genetische algoritmen. De waardes in het veld zijn allemaal in de vorm 2^n wat een exponentieel verband is. Dit vindt het netwerk lastig om mee om te gaan en daarom is gekozen om de input te transformeren. Om er een lineair verband van te maken is in eerste instantie alleen de macht (n) als input genomen. Dit zorgde ervoor dat het leerproces 4x sneller werd. Vervolgens zijn deze waardes genormaliseerd wat het leerproces ruim 5x sneller maakte in vergelijking met het gebruik van de exponentiele waardes.
Verder is 2048 een spel dat redelijk wat onzekerheid heeft in de vorm van de nieuwe tegels (plaats + waarde). Stel een bepaald model in de populatie kan alleen omgaan met één soort situatie en de willekeur zorgt ervoor dat dit model precies die situatie krijgt zal de fitness erg hoog zijn. Dit terwijl het model eigenlijk geen flexibiliteit kent. Dit kan ook andersom gebeuren, waarbij een model dat erg goed is in 95% van de situaties precies de 5% krijgt waar het model slecht mee om weet te gaan. Om deze willekeur enigszins te elimineren moest elk model drie spellen spelen en werd de gemiddelde fitness genomen als eind fitness.
Ten slotte, hoe verder je in het spel komt des te lastiger wordt het om een hogere tegel te verkrijgen. Voor het halen van een tegel met waarde 16 heb je twee tegels van 8 nodig. Om twee tegels van 8 te verkrijgen zijn vier tegels van 4 nodig enzovoort. Dit is relatief makkelijk vergeleken met het behalen van een tegel met bijvoorbeeld waarde 512. Dit is hoe het spel is opgebouwd en maakt 2048 juist zo uitdagend.


