Obviously to cheer on Max Verstappen, but at the same time I try to beat family members with the NU.nl GP-game.
Although I am sure I am the áll greatest Formula 1 connoisseur within my family, I often let math give me a hand.
How does the GP game work?
Each weekend a race is held in a different country, consisting of a qualifying race and an official race.
For each race weekend, participants must put together a team of four drivers and predict the top three.
In addition, you can score extra points by correctly predicting Max Verstappen’s position.
In this blog, I share how I used mathematical models to optimize my team of four drivers.
I will leave out predicting qualifying and the race this time, although that is an interesting data science application.
To put together a team consisting of four drivers, you have a total budget of 100 million available.
NU.nl’s team determined the costs for the various drivers, with the better the driver, the more expensive.
For example, Lewis Hamilton costs as much as 50 million, while Mick Schumacher – son of – costs “only” 5 million.
You earn points based on the positions of the drivers in your team after qualifying and the race.
For example, if Max Verstappen is in your team and takes pole position on Saturday and wins the race on Sunday, you will earn (10 for pole position + 25 for race win) 35 points.
The goal, of course, is to collect as many points as possible with your selected team.
Knapsack problem
The above problem involving choosing the optimal team of drivers is a so-called knapsack problem.
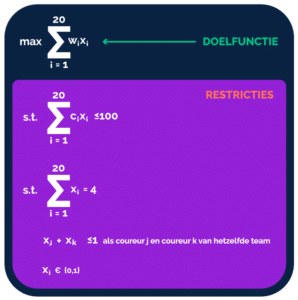
The knapsack problem is a well-known mathematical problem involving the following question: ‘Given a collection of items I, where each item i has an associated weight c_i and an associated value w_i.
Determine which objects should be included in the knapsack so that the value is as high as possible but the maximum weight is not exceeded.’
At the same time, the maximum weight must not be exceeded; we call this a constraint.
GP game as knapsack problem
Assembling a team of drivers can now be formulated as a knapsack problem.
Namely, given is a set of drivers I, with certain cost c_i for each driver.
The goal is to maximize the total value of the team.
However, the value generated by each driver is not known, so we have to come up with something “clever” for that (I will come back to this later).
In addition to the budget of 100 million, there are a few additional restrictions from the game that we need to take into account, namely:
- From each team you may choose a maximum of one driver.
- You have to choose exactly four drivers.
- The solution to the problem is binary; you choose a driver either (1) or not (0).
GP game as ILP problem
The next step is to formulate our mathematical problem as a integer linear programming problem.
Indeed, it is well known within our field that a knapsack problem can be solved using linear programming.
Linear programming is a method for solving optimization problem in which the target function and constraints are linear.
This is also the case in our problem.
In addition, we speak here of a integer linear programming problem because the solution is binary (and therefore integer).
Namely, for each driver i, we define a decision variable x_i.
This variable is equal to 1 if driver i is chosen in the solution, but equal to 0 if we do not choose him.
We can then formulate our problem as a integer linear programming problem (beware: mathematical formulas alert!).
As mentioned earlier, we want to maximize the value of our team.
Therefore, for each driver i (20 in total) we determine a value w_i.
This value is determined based on the current standings in the championship and the results of the free practice sessions.
Thus, I include both the performance of a driver during the season and during the race weekend.
For example, Max Verstappen’s value during the race weekend in Austria (from July 2 to 4, 2021) can be determined as follows: Number of points in the championship on July 3, 2021: 156 points championship (FP) Position free practice 1: 1 (P1) Position free practice 2: 3 (P2) Position free practice 3: 1 (P3) Value Max: KP + (21 – P1) + (21 – P2) + (21 – P3) = 156 + (21 – 1) + (21 – 3) + (21 – 1) = 214 The value of the selected team can be determined by taking the sum of the value of the drivers on the team.
Note that this corresponds to the goal function in our mathematical formulation above since the variable x_i is equal to 0 if we do not have a driver in our team.
What follows are the constraints.
Constraint 1 says that the total cost of all the drivers we choose in our team cannot exceed the budget of 100 million.
We calculate the total cost by taking the sum of the cost per driver i on our team, c_i.
The same reasoning applies as for the goal function: if we do not choose a driver in our team, the variable x_i equals 0 and we do not count that cost.
Constraint 2 enforces that we select exactly four drivers in our team.
The third constraint enforces that we select at most 1 driver per team.
Suppose driver j is Max Verstappen (team Red Bull) and driver k is Sergio Perez (also team Red Bull), then this constraint says that the sum of the decision variables can be at most 1.
This means that we cannot choose both drivers (because then x_j + x_k = 2).
Calculate optimal solution
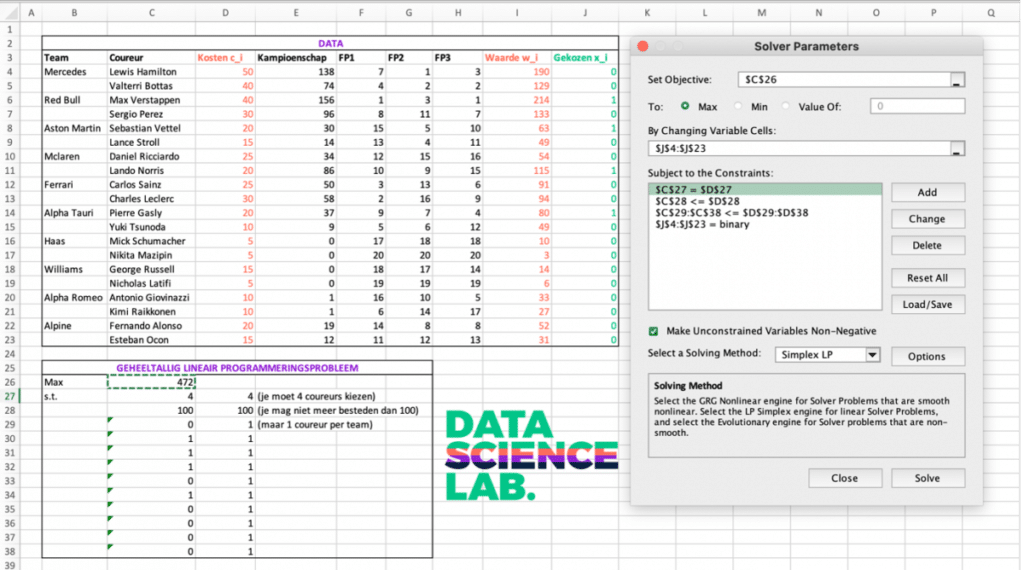
For modeling this time I choose not Python or R, but Excel.
This is because in Excel you can easily formulate and solve linear programming problems using the Solver.
Below you can see a screenshot of my Excel sheet.
Then we use the data to specify our integer linear programming problem.
We need to fill in the right cells in the right place in the Solver:
- Target Function (‘Set Objective’) The target function is found in cell C26.
This cell contains the following formula: SUMPRODUCT(I4:I23, J4:J23).
We want to maximize the objective function.
- Decision Variables (‘By Changing Variable Cells’) The decision variables are found in cells J4:J23.
- Constraints (‘Subject to the Constraints’) Here we add all constraints:
| Restriction | Cells | Formula in Excel |
| You have to choose 4 drivers | C27 <= D27 | SUM(J4:J23) <= 4 |
| You cannot spend more than 100 million | C28 <= D28 | SUMPRODUCT(D4:D23,J4:J23) <= 100 |
| You may only choose 1 driver per team | C29:C38 <= D29:D38 | For example, SUM(J4:J5) <= 1 for Mercedes. |
| Decision variables binary | J4:J23 | J4:J23 = binary |
Next, we can specify in the Solver which algorithm we want to use to solve the problem.
We choose Simplex LP because our target function and constraints are linear.
We then get back the following optimal solution:
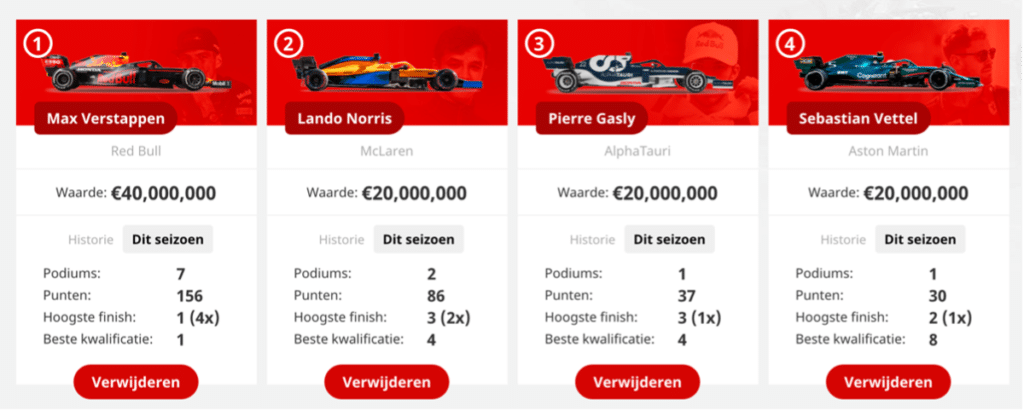
I decide to rely completely on my model for the race weekend in Austria and choose these drivers in my team.
Fingers crossed…
Was this the best team?
Now that the race weekend in Austria is over, we can take stock: did the model choose the best team?
We can calculate this based on the results of qualifying and the race.
Indeed, in total, my team achieved 69 points, 27 for qualifying and 42 for the race.
Now we can again have the optimal team calculated by the model, namely by taking as a value the points distribution of the GP game based on the results for qualification and the race.
Then we get the following optimal team as a solution:
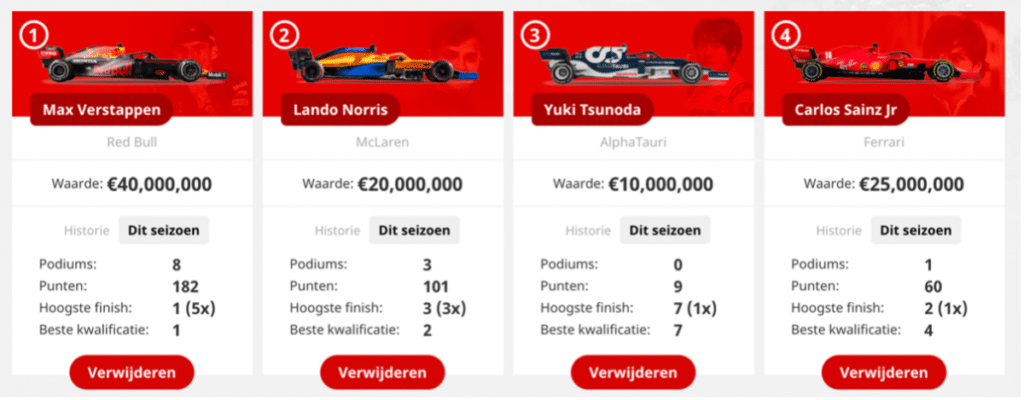
What is beyond doubt is that you should have chosen Max Verstappen and Lando Norris in your team, because together they already provide 49 points.
Unfortunately, in retrospect, the model did not choose the optimal team for the race weekend in Austria.
This is not due to our model itself or the simplex method, but because we estimated the value of the drivers prior to qualifying using the value function.
However, to determine if the model is statistically better than a human participant, we obviously need to look at more than one race weekend.
One thing is certain: in our family pool, I scored the most points with my team.
Points of improvement
Of course, there are still a number of possible improvements to my model, especially when it comes to determining the value of drivers.
For example, the calculation could be extended to include qualifying results or performance at similar tracks.
In addition, it might be interesting to investigate whether the weighted function is the best choice for determining value.
The value function could possibly be optimized using machine learning or by viewing the value as stochastic rather than deterministic.
Especially the latter could add a lot of value to the model, since luck and bad luck can play a big role in Formula 1.
Applications of linear programming
Linear programming has all kinds of applications in business.
Think of the optimal combination of products a company should produce to make the most profit, creating a work schedule for hospital staff, finding the shortest route from A to B or solving a transportation problem.
I believe that operations research techniques, such as linear programming, are still underutilized within the world of data science.
Sometimes the most complicated neural networks are trained, while the same question can be answered with a much simpler model.
In our work, therefore, we must always keep making the trade-off between complexity and effectiveness.
Whether my model is effective enough to win NU.nl’s F1 game?
We will know at the end of this Formula 1 season ;).