Hoe werkt het GP-spel?
Het GP-spel is ontwikkeld door NU.nl en beslaat één Formule 1 seizoen. Ieder weekend wordt een race in een ander land gereden, bestaande uit een kwalificatiewedstrijd en een officiële wedstrijd. Voor ieder raceweekend moeten deelnemers een team van vier coureurs samenstellen en de top 3 voorspellen. Daarnaast kun je extra punten scoren door de positie van Max Verstappen correct te voorspellen. In deze blog vertel ik hoe ik wiskundige modellen heb ingezet om mijn team van vier coureurs te optimaliseren. Het voorspellen van de kwalificatie en de race laat ik ditmaal buiten beschouwing, hoewel dat een interessante data science toepassing is.
Voor het samenstellen van een team bestaande uit vier coureurs, heb je een budget van in totaal 100 miljoen beschikbaar. Het team van NU.nl heeft voor de verschillende coureurs de kosten bepaald, waarbij geldt: hoe beter de coureur, hoe duurder. Zo kost Lewis Hamilton maar liefst 50 miljoen, terwijl Mick Schumacher – zoon van – ‘slechts’ 5 miljoen kost. Je verdient punten op basis van de posities van de coureurs in je team na de kwalificatie en de race. Bijvoorbeeld: wanneer Max Verstappen in jouw team zit en pole position pakt op zaterdag en de race wint op zondag, verdien je (10 voor pole position + 25 voor winst race) 35 punten. Het doel is uiteraard om zoveel mogelijk punten te verzamelen met jouw geselecteerde team.
Knapzakprobleem
Het bovengenoemde probleem waarbij de keuze gemaakt moet worden voor het optimale team van coureurs, is een zogeheten knapzakprobleem. Het knapzakprobleem is een bekende wiskundige kwestie waarbij de volgende vraag centraal staat:
‘Gegeven is een verzameling items I, waarbij elk item i een bijbehorend gewicht c_i en een bijbehorende waarde w_i heeft. Bepaal welke objecten meegenomen moeten in de knapzak, zodat de waarde zo hoog mogelijk is maar het maximale gewicht niet wordt overgeschreden.’

GP-spel als knapzakprobleem
Het samenstellen van een team coureurs kan nu geformuleerd worden als knapzakprobleem. Gegeven is namelijk een verzameling coureurs I, met voor elke coureur bepaalde kosten c_i. Het doel is om de totale waarde van het team te maximaliseren. De waarde die iedere coureur oplevert is echter niet bekend, dus daar moeten we iets ‘slims’ op verzinnen (hier kom ik later op terug). Naast het budget van 100 miljoen zijn er nog een paar extra restricties vanuit het spel waar we rekening mee moeten houden, namelijk:
- Uit elk team mag je maximaal één coureur kiezen.
- Je moet exact vier coureurs kiezen.
- De oplossing van het probleem is binair; je kiest een coureur wel (1) of niet (0).
GP-spel als ILP probleem
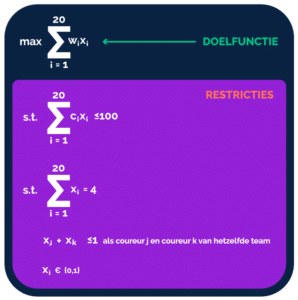
De volgende stap is het formuleren van ons wiskundige probleem als een geheeltallig lineair programmeringsprobleem. Het is namelijk binnen ons vakgebied bekend dat een knapzakprobleem opgelost kan worden met behulp van lineair programmeren. Lineair programmeren is een methode voor het oplossen van optimaliseringsprobleem, waarin de doelfunctie en de restricties lineair zijn. Dat is ook bij ons probleem het geval. Daarnaast spreken we hier van een geheeltallig lineair programmeringsprobleem omdat de oplossing binair is (en dus geheeltallig). We definiëren namelijk per coureur i een beslissingsvariabele x_i. Deze variabele is gelijk aan 1 als coureur i gekozen wordt in de oplossing, maar gelijk aan 0 als we hem niet kiezen. We kunnen ons probleem dan als een geheeltallig lineair programmeringsprobleem formuleren (pas op: wiskundige formules alert!).
Aantal punten in het kampioenschap op 3 juli 2021: 156 punten kampioenschap (KP)
Positie vrije training 1: 1 (P1)
Positie vrije training 2: 3 (P2)
Positie vrije training 3: 1 (P3)
Waarde Max: KP + (21 – P1) + (21 – P2) + (21 – P3) = 156 + (21 – 1) + (21 – 3) + (21 – 1) = 214
De waarde van het geselecteerde team kan worden bepaald door de som te nemen van de waarde van de coureurs in het team. Merk op dat dit overeenkomt met de doelfunctie in onze wiskundige formulering hierboven aangezien de variabele x_i gelijk is aan 0 als we een coureur niet in ons team hebben.
Wat volgt zijn de restricties. Restrictie 1 zegt dat de totale kosten van alle coureurs die we kiezen in ons team het budget van 100 miljoen niet mag overschrijden. De totale kosten berekenen we door de som te nemen van de kosten per coureur i in ons team, c_i. Dezelfde redenering geldt als bij de doelfunctie: als we een coureur niet in ons team kiezen, is de variabele x_i gelijk aan 0 en tellen we die kosten niet mee. Restrictie 2 dwingt af dat we exact vier coureurs in ons team selecteren. De derde restrictie dwingt af dat we maximaal 1 coureur per team kiezen. Stel: coureur j is Max Verstappen (team Red Bull) en coureur k is Sergio Perez (óók team Red Bull), dan zegt deze restrictie dat de som van de beslissingsvariabelen maximaal 1 kan zijn. Dit betekent dat we niet beide coureurs kunnen kiezen (want dan geldt x_j + x_k = 2).
Optimale oplossing berekenen
Voor het modelleren kies ik dit keer niet voor Python of R, maar voor Excel. In Excel kun je namelijk makkelijk lineaire programmeringsproblemen formuleren en oplossen met behulp van de Solver. Hieronder zie je een screenshot van mijn Excel sheet.
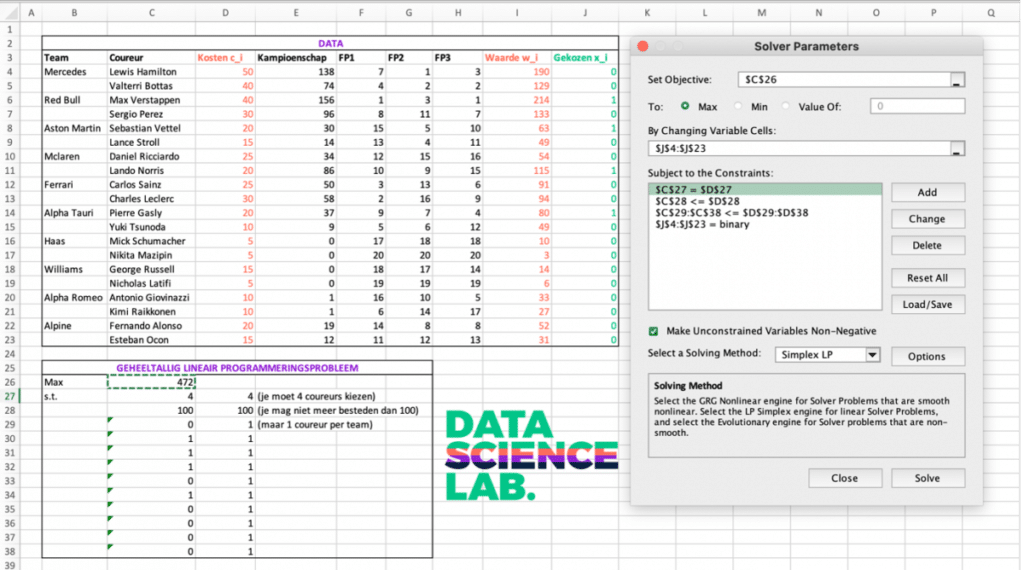
- Doelfunctie (‘Set Objective’)
De doelfunctie is terug te vinden in cel C26. Deze cel bevat de volgende formule: SUMPRODUCT(I4:I23, J4:J23). We willen de doelfunctie maximaliseren.
- Beslissingsvariabelen (‘By Changing Variable Cells’)
De beslissingvariabelen zijn terug te vinden in de cellen J4:J23. - Restricties (‘Subject to the Constraints’)
Hier voegen we alle restricties toe:
| Restrictie | Cellen | Formule in Excel |
| Je moet 4 coureurs kiezen | C27 <= D27 | SUM(J4:J23) <= 4 |
| Je mag niet meer besteden dan 100 miljoen | C28 <= D28 | SUMPRODUCT(D4:D23,J4:J23) <= 100 |
| Je mag maar 1 coureur kiezen per team | C29:C38 <= D29:D38 | Bijvoorbeeld SUM(J4:J5) <= 1 voor Mercedes. |
| Beslissingsvariabelen binair | J4:J23 | J4:J23 = binary |
Vervolgens kunnen we in de Solver aangeven met welk algoritme we het probleem willen oplossen. We kiezen Simplex LP omdat onze doelfunctie en restricties lineair zijn. We krijgen dan de volgende optimale oplossing terug:
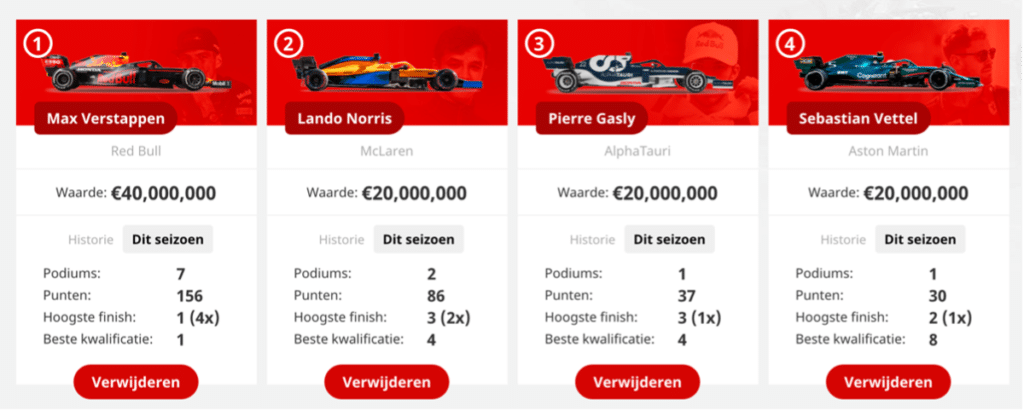
Was dit het beste team?
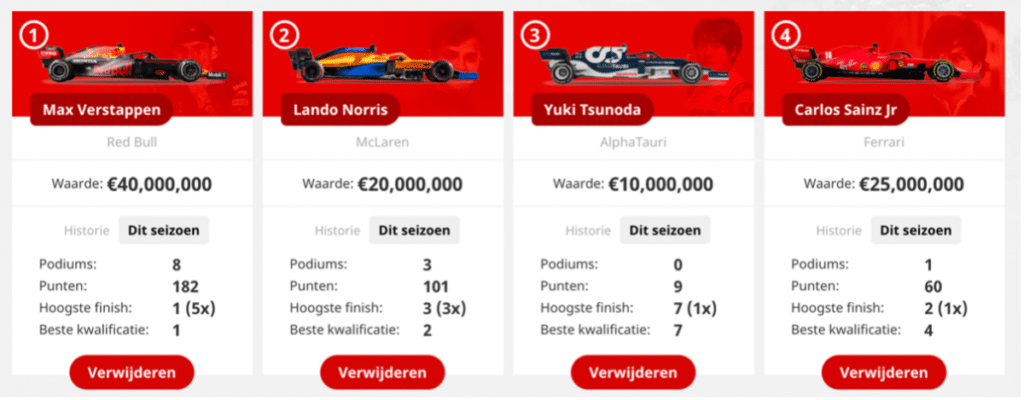
Nu het raceweekend in Oostenrijk achter de rug is, kunnen we de balans opmaken: heeft het model het beste team gekozen? Dit kunnen we berekenen op basis van de uitslag van de kwalificatie en de race. In totaal heeft mijn team namelijk 69 punten gehaald, 27 voor de kwalificatie en 42 voor de race. We kunnen nu opnieuw het optimale team laten berekenen door het model, namelijk door als waarde de puntenverdeling van het GP-spel te nemen op basis van de uitslag voor de kwalificatie en de race. Dan krijgen we het volgende optimale team als oplossing:
Verbeterpunten
Uiteraard zijn er nog een aantal verbeteringen mogelijk aan mijn model, met name als het gaat om het bepalen van de waarde van de coureurs. Zo kan de berekening bijvoorbeeld worden uitgebreid met kwalificatieresultaten of prestaties op soortgelijke circuits. Daarnaast zou het interessant kunnen zijn om te onderzoeken of de gewogen functie wel de beste keuze is om de waarde te bepalen. De waarde functie zou eventueel geoptimaliseerd kunnen worden met behulp van machine learning of door de waarde te zien als stochastisch in plaats van deterministisch. Vooral dat laatste kan veel toegevoegde waarde hebben voor het model, aangezien geluk en pech een grote rol kunnen spelen in de Formule 1.
Toepassingen van lineair programmeren
Lineair programmeren heeft allerlei toepassingen in het bedrijfsleven. Denk aan de optimale combinatie van producten die een bedrijf moet produceren om de meeste winst te maken, het opstellen van een werkrooster voor ziekenhuispersoneel, het vinden van de kortste route van A naar B of het oplossen van een transportprobleem. Ik ben van mening dat operations research technieken, zoals lineair programmeren, nog te weinig worden ingezet binnen de wereld van data science. Soms worden de meest ingewikkelde neurale netwerken getraind, terwijl dezelfde vraag kan worden beantwoord met een veel simpeler model. In ons werk moeten we daarom altijd de afweging blijven maken tussen complexiteit en effectiviteit. Of mijn model effectief genoeg is om het F1 spel van NU.nl te winnen? Dat weten we aan het einde van dit Formule 1 seizoen ;).